Konferencja Inspiracje 2016 – moje wystąpienie

30 czerwca – 1 lipca 2016 roku w Warszawie odbyła się Konferencja Innowacyjnych Nauczycieli i Edukatorów

pt. „INSPIR@CJE 2016 – JAK UCZYNIĆ POLSKĄ SZKOŁĘ JESZCZE LEPSZĄ?”.

W swoim wystąpieniu opowiedziałam w jaki sposób pracuję z uczniami używając kości do gry.

Tytuł wystąpienia brzmiał „Matematyka z kośćmi – zagrajmy, aby się uczyć”.

Tu informacje o konferencji: http://www.edunews.pl/wydarzenia/3345-inspiracje-2016-konferencja

O CZYM MÓWIŁAM?

Prezentowane przeze mnie przykłady gier i zabaw oraz wiele innych przykładów znajdziecie Państwo na podanych stronach internetowych: moja strona – matematykawpodstawowce.pl oraz blog tworzony przez nauczycielki z grupy Superbelfrzy Mini – kostkinamatmie.edu.pl

Wprowadzając zabawy z kośćmi w nowej klasie, zajęcia rozpoczynam od krótkiego opowiadania o początkach kości do gry. Historia kości jest niemal tak długa, jak historia ludzkości. Jest to prawdopodobnie najstarsze z narzędzi służących do gry znane człowiekowi. Kości, choć trochę inne niż obecnie, znane były w starożytnej Grecji, Rzymie, czy Egipcie. Były także ulubioną rozrywką rycerstwa w epoce średniowiecza. Początkowo funkcję kości do gry spełniały kości skokowe zwierząt hodowlanych, mające kształt zbliżony do czworościanu. Później wykorzystywano różne materiały, takie jak: pestki owoców, nasiona, kość słoniową, szkło czy metal.

Kości dziś mają wiele zastosowań i wyglądają przeróżnie, liczba ścianek sięga od 4 do 100. Najczęściej spotykane są kości sześcienne, ale staram się z uczniami rozmawiać na temat innego możliwego kształtu. Dzieci szybko odkrywają, że każda ścianka kostki musi być taka sama, czyli tej samej wielkości i o takim samym kształcie.

Uwielbiam prace manualne, w klasie mam różne papierowe modele brył, także wielościanów archimedesowych i wielościanów catalana. Oglądając, uczniowie wybierają te wielościany, z których mogłaby powstać kostka do gry.

Przygotowałam w geogebrze siatki przykładowych kostek do gry. Szablony siatek dostępne są do pobrania na mojej stronie – Matematyka w podstawówce – SZABLONY SIATEK KOŚCI

Siatki drukowałam na kartach z bloku technicznego, uczniowie kolorowali i tworzyli przeróżne, unikalne wzory.

Moi uczniowie tworzyli swoje kostki w kształcie czworościanu, sześcianu i ośmiościanu. Wycinali, zaginali dokładnie wszystkie krawędzie…

… i składali.

Wiemy doskonale, że gdy uczniowie działają praktycznie, np. tworzą czy składają zapamiętują najwięcej. Dodatkowo można później grać własnoręcznie wykonaną kostką.

Zaprezentowałam magiczną sztuczkę – takie czary.

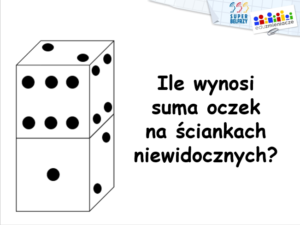
Zaczynam od rzutu dwiema kostkami sześciennymi. Buduję z nich wieżę. Nie zaglądając, nie oszukując, potrafię podać sumę oczek na niewidocznych ściankach kostek.

Uczniowie, którzy sumiennie oglądali kostkę sześcienną potrafią szybko wpaść na sposób rozwiązania tej sztuczki. Niektórym zajmuje to trochę czasu lub trzeba ich naprowadzać.

Spróbowaliśmy się zabawić? Nagrodą były unikalne kostki, stworzone przez moich uczniów.

Przypomniałam, rzucam dwiema sześciennymi kostkami, układam z nich wieżę. Zadanie polega na odgadnięciu sumy oczek na ściankach niewidocznych utworzonej wieży?

Kto znalazł rozwiązanie, podnosił ręki do góry.

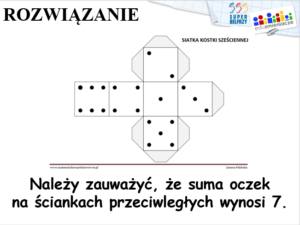
Wieża 1 – rozwiązanie to 12

Wieża 2 – rozwiązanie to 15

Należy zauważyć, że suma oczek na ściankach przeciwległych wynosi 7.

Warto przy tej magicznej sztuczce zatrzymać się na chwilkę i kontynuować rozważania, poprosić uczniów, aby spróbowali sformułować własne pytania do zbudowanej wieży, np.

Jaka może być największa suma oczek, a jaka najmniejsza na ściankach widocznych?
Jaka może być największa suma oczek, a jaka najmniejsza na ściankach niewidocznych?
Czy można zbudować wieżę z trzech kostek sześciennych, w której suma oczek na ścianach widocznych wyniesie 29? Itd.

W dalszej części zaprezentowałam kilka przykładów wykorzystania na lekcjach matematyki kości.

TABLICZKA MNOŻENIA

Potrzebujemy: planszę dla każdej pary, 10 żetonów w 2 kolorach oraz 2 kostki dziesięciościenne 0 – 9.

Rzucamy na zmianę dwiema kostkami i kładziemy żeton na wyniku mnożenia. Wygrywa ten, kto pierwszy położy na planszy wszystkie swoje żetony. Na jednym polu może stać tylko jeden żeton. Plansza do pobrania dostępna jest na prezentowanych wcześniej stronach.

W każdej z prezentowanych gier możliwe są modyfikacje, warto z uczniami rozmawiać i prosić i o swoje pomysły wykorzystania tej planszy.

ODEJMOWANIE – POWOLNY WYŚCIG

Potrzebujemy: 2 kostki do gry, kartkę do zapisu liczb. Każdy gracz ma w puli 100 punktów. W jednym ruchu gracz rzuca dwiema kostkami i tworzy z wyrzuconych oczek liczbę dwucyfrową (np. gdy wyrzuci 2 i 4 oczka, może utworzyć liczbę 24 lub 42). Liczbę tę gracz odejmuje od liczby posiadanych punktów. Gracze wykonują ruchy na zmianę. Przegrywa ten gracz, który jako pierwszy straci wszystkie punkty lub utworzona przez niego liczba będzie większa od liczby posiadanych punktów.

DRUGA POTĘGA

Potrzebujemy: żetony w 2 kolorach, planszę z ponumerowanymi polami, ja wykorzystałam kostki dziesięciościenne, więc trenowaliśmy drugą potęgę liczb od 0 do 9. Rzucamy kostką i obliczamy drugą potęgę z wartości wyrzuconej na kostce. Po wyrzuceniu np. 4 przykrywamy żetonem pole 16, bo 4 x 4 = 16. Rzucamy na zmianę, wygrywa osoba, która pierwsza przykryje wszystkie komórki.

POTĘGOWANIE

Potrzebujemy: dowolne dwie kostki i kartkę do zapisu. Rzucamy dwiema kostkami do gry. Sami decydujemy, która z wyrzuconych oczek to podstawa potęgi, a która to wykładnik. Obliczamy potęgę.

POLE PROSTOKĄTA

Potrzebujemy: kartkę w kratkę oraz 2 kostki. Uczniowie rzucają dwiema kostkami do gry. Liczba wyrzuconych oczek to długości boków prostokąta. Obliczają pole prostokąta. Wygrywa ten, kto pierwszy zapełni całą swoją część kartki.

OBJĘTOŚĆ I POLE POWIERZCHNI

Potrzebujemy: dowolne trzy kostki i kartkę do zapisu. Rzucamy trzema kostkami do gry. Liczba wyrzuconych oczek to wymiary prostopadłościanu: długość, szerokość i wysokość. Obliczamy objętość prostopadłościanu i jego pole powierzchni.

KOLEJNOŚĆ DZIAŁAŃ

Potrzebujemy: kartkę do zapisu i rzutnik lub kości. Uczniowie rzucają trzema kostkami do gry lub nauczyciel korzysta z rzutnika i wyświetla wirtualny rzut trzema kostkami. Z otrzymanych na kostkach oczek tworzymy działanie, które da: – najwyższy wynik, – najniższy wynik… Prosimy uczniów o podawanie przykładów poleceń do wykonania.